BGMの周波数を分析する（minim編）

◆PROCESSING　逆引きリファレンス

　カテゴリー：音楽・演奏

【解説】

minimは、PROCESSINGで手軽に音楽を演奏できるライブラリです。

minimについて、より詳しく知りたい方は下記公式サイト様を参照して下さい。

音楽プレーヤーの中には、音楽の再生と共に音の強弱を周波数単位のグラフとして表示してくれるものがあります。

（画像URL：9ineBB 様）

これをスペクトラムアナライザと呼びます。

スペクトラムアナライザを minim で実現するためには、minimが持つ FFT（高速フーリエ変換）の機能を利用します。

音楽におけるフーリエ変換とは何か・・・について、理工系ではない私には正確に説明する事ができません（汗）。

しかし理解した範囲で書かせて頂くなら、時系列に変化する音の強弱を、周波数単位に変化する音の強弱に変換するもののようです。

例えば2Hz（１秒間に2回同じ波形を繰り返す）sin波と6Hzのsin波があったとして、この2つを足し算すると、少し複雑な波形が出来上がります。

この足し算して出来上がった波形をもとに、これが何Hzと何Hzの波が合わさったものかを計算するのがフーリエ変換です。

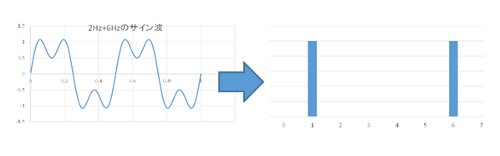
この計算を行うには、minimがサポートする FFTクラスの命令を利用します。

【構文】

●インスタンス変数を生成する

FFT fft = new FFT( int bufferSize, int sampleRate ) ;

bufferSize : 　分析する音楽ファイルのサンプリングバッファ・サイズを与えます。
sampleRate：分析する音楽ファイルのサンプリング・レートを与えます。

●窓関数を指定する
void fft . window( WindowFunction wFunction ) ;

wFunction には以下の指定が可能です。

FFT.NONE 指定なし
FFT.BARTLETT バートレット窓
FFT.BARTLETTHANN バートレット・ハン窓
FFT.BLACKMAN ブラックマン窓
FFT.COSINE コサイン（テューキー）窓
FFT.GAUSS ガウス窓
FFT.HAMMING ハミング窓
FFT.HANN ハン（ハニング）窓
FFT.LANCZOS ランツォシュ窓
FFT.TRIANGULAR 三角窓（バートレット窓といっしょ？）

●FFT解析を行う
void fft . forward( AudioBuffer buffer ) ;

bufferには解析したいAudioBuffer 型の変数を与えます。

●周波数帯域数を取得する
int specSize = fft . specSize() ;

●周波数帯域の幅（Hz）を取得する
float bandWidth = fft . getBandWidth() ;

●周波数帯域ごとの振幅を取得する
float getBand = fft . getBand( int specIndex ) ;

specIndex ：振幅を取得したい帯域位置

【注意】

minimでFFT解析を行うには、プログラムの先頭に
import ddf.minim.*;
import ddf.minim.analysis.*;
などと記述して、ライブラリの利用宣言を行う必要があります。

インスタンス変数を作成する

MinimでFFT解析を行うには、FFTクラスのインスタンス変数を作成する必要があります。

FFTクラスのインスタンス変数を作成するには、FFTクラスのコンストラクタに分析したい音データのサンプリングバッファ・サイズとサンプリング・レートを与えます。

mp3 などの音楽データを解析するのであれば、サンプリングバッファ・サイズとサンプリング・レートは、音楽ファイルをMinimに読み込ませた際に戻される AudioPlayer型のインスタンス変数がもつメソッドで取得可能です。

例えば
AudioPlayer player = minim.loadFile ( “hoge.mp3” ) ;
としているなら
player. bufferSize() ; 　でサンプリングバッファ・サイズが
player.sampleRate() ; でサンプリング・レートが
取得できます。

窓関数を指定する

この操作を行わなくても、音波を周波数に変換できます。

がコンピュータでFFT解析を行う時には、解析したい波の種類に応じて窓関数を指定するのが一般的なのだそうです。・・・窓関数って何？・・・とは聞かないでくださいね。私は、よくわかりません（汗）。

（理解した範囲でざっくり書くと）フーリエ変換は、周期性のある無限に繰り返される波を解析するのが前提ですが、周期性が成り立たない有限個のデータを変換する場合、特有のブレが発生します。

窓関数は、このブレを緩和するもの・・・のようです。ええ・・・たぶん（orz）。窓関数については

などを参照してください。

音波をFFT変換する場合は、ハニング窓（FFT.HANN）かハミング窓（FFT.HAMMING）を利用するようです。

FFT解析を行う

FFTクラスが持つ forward() メソッドに、解析したいAudioBuffer型の変数を与えます。

mp3 などの音楽データを解析するのであれば、AudioBufferは音楽ファイルをMinimに読み込ませた際に戻される AudioPlayer型のインスタンス変数が持つプロパティを利用します。

例えば
AudioPlayer player = minim.loadFile ( “hoge.mp3” ) ;
としているなら
player . left　左チャネル音データ
player . right　右チャネル音データ
player . mix　左右混合音データ
のいずれかを指定します。

周波数帯域数を取得する

specStep() で、いくつの周波数帯域に分割して解析できるのかを取得します。

その音楽ファイルのサンプリングレート（44100Hzなど）を、specStep() 個の周波数に分割して解析が行えるという事です。

したがって本命令から戻される値は、解析する音源のサンプリングレートやバッファサイズに左右されます。

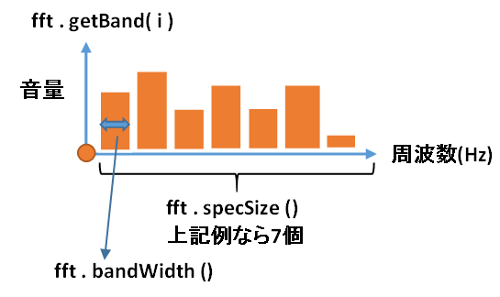
より具体的には、例えば44100Hzの音楽データをサンプリングバッファサイズ＝1024個で解析する場合、specSize() には513（513個に分割できる）が戻されます。

周波数帯域の幅（Hz）を取得する

getBandWidth() で得られる値は、上記 specSize() で分割する1つ1つの周波数帯域の大きさを示します。上図で言えば、赤い棒グラフが何ヘルツ分の幅を持っているかを示しています。

戻される値は、解析する音源のサンプリングレートやバッファサイズに左右されます。

例えば44100Hzの音楽データをサンプリングバッファサイズ＝1024個で解析する場合、getBandWidth() には43が戻されます。これは、43Hz ✕ 513個 = 22059Hz までの音域が解析できる事を示しています。

mp3などの音楽ファイルでは、サンプリングレートが44100Hzであっても、その半分（人間の可聴領域＝約20000Hz）までの音しか入っていません。その為、getBandWidth() には期待する半分の大きさが戻されるようです。

周波数帯域ごとの振幅を取得する

getBand() で、0から specStep() -1 個までの周波数帯域の音量を取得可能です。

どの位置の音量を得たいかを、getBand()の引数に指定します。戻される振幅をレベル（ｄB）に変換するには下記計算式を用います。

float dB = 20 * ( (float)Math.log10( fft.getBand( i ) ) ;

たぶん・・・あっていると思いますが、ちょっと自信がありません（汗）。違っていたらごめんなさい。その時は、やさしく教えてください。

振幅とｄBについては、下記サイト様などが参考となります。

【関連記事】

サンプルプログラム

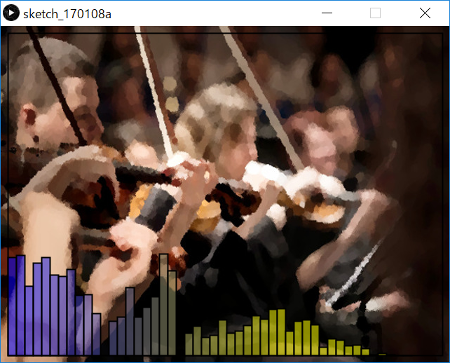
スペクトラムアナライザの例：

import ddf.minim.*;
import ddf.minim.analysis.*;

//棒グラフを描く数
//下記 bandHzの要素数以下である必要があります。
final int MAXBAND = 48;          

//グローバル変数
Minim       minim;               //minimオブジェクト
AudioPlayer player;              //演奏クラス
FFT         fft;                 //FFT解析クラス
float     specSize;              //周波数分解幅
float     initBand;              //分解Hz
int       stepCount;             //表示するサンプリング単位幅
int       wakuX, wakuY;          //外枠の描画原点
int       wakuWidth, wakuHeight; //外枠の幅と高さ
int       barWidth;              //棒グラフの幅
PImage    back;                  //背景画像

//以下の48個のHz単位に棒グラフを描く
int       bandHz[] =  {   43,   43,   43,   43,   43,   43,   43,    43, 
                          43,   43,   43,   43,   43,   43,   43,    43,
                          86,   86,   86,   86,   86,   86,   86,    86,
                         172,  172,  172,  172,  688,  688,  688,   688,
                         215,  215,  344,  344,  516,  516,  688,   688,
                        1032, 1032, 1204, 1376, 1548, 1720, 1892,  2064 };
void setup() {
  size( 640, 480 );
  //画面中央にスペクトルグラフを描画する
  wakuX = 10;
  wakuY = 10;
  wakuWidth = 620;
  wakuHeight = 460;
  
  back = loadImage( "ensoukai.jpg" );
  
  //音楽読み込み
  minim = new Minim(this);
  player = minim.loadFile("castle-the-order.mp3"); 

  //FFT設定
  fft = new FFT( player.bufferSize(), player.sampleRate()); 
  
  //周波数分解幅を取得
  //全周波数を、この数の個数に分割して分析可能。通常は513
  specSize = fft.specSize();

  //HANN窓指定。minimではHAMMINGより精度が高そう・・・
  fft.window( FFT.HANN );
    
  //初期分解Hz(getBandWidth)を求める
  //分解幅1つ単位のHz。
  //例えば分解Hzが 43 なら、43 × 513 = 22059Hzまで解析可能
  initBand = fft.getBandWidth();
  
  //棒グラフの幅
  barWidth = wakuWidth / MAXBAND;

  //音楽再生
  player.play();
}

void draw() {   
  background( back );
  
  //スペクトルを描画する範囲の外枠を描く 
  strokeWeight( 2 );
  stroke( 0 );
  noFill();
  rect( wakuX, wakuY, wakuWidth, wakuHeight );

  if( player.isPlaying() == false ){
    return;
  }
    
  //FFT開始(左右混合分析)
  //左のみなら player.left、右のみなら player.right を指定
  fft.forward( player.mix );
  
  int ToStep = 0;      //ここから
  int FromStep = 0;    //ここまでの振幅を平均する
  
  //スペクトルグラフ描画
  for( int index = 0; index < MAXBAND; index++ ){
    //指定されたHz単位の平均を採取するため
    //計算範囲を求める   
    int bandStep = (int)( bandHz[index] / initBand );
    if( bandStep < 1 ){ bandStep = 1; }
    
    ToStep = ToStep + Math.round( bandStep );
    if( ToStep > specSize ){ ToStep = (int)specSize; }   
    
    //平均値を計算
    float bandAv = 0;
    for( int j = FromStep ; j < ToStep; j++ ){      
      //振幅をDBに変換
       float bandDB = 0; 
      if ( fft.getBand( j ) != 0 ) {   
        bandDB = 2 * ( 20 * ((float)Math.log10(fft.getBand(j))) + 40);
        if( bandDB < 0 ){ bandDB = 0; }
      }      
      bandAv = bandAv + bandDB;
    }    
    bandAv = bandAv / bandStep;  //平均値
    FromStep = ToStep;
    
    //グラフの描画座標を計算
    float y = map( bandAv, 0, 250, 0, wakuHeight ); 
    if( y < 0) { y = 0; }

    //グラフの色を計算
    color c1 = color( 0,0,255 );
    color c2 = color( 255,255,0 );    
    color c3 = lerpColor( c1, c2, index/32.0 );
    fill( c3, 140 );    

    //棒グラフを描画
    rect( index*barWidth+wakuX,( wakuHeight-y )+wakuY, barWidth, y );
  } 
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

import ddf.minim.*;

import ddf.minim.analysis.*;

//棒グラフを描く数

//下記 bandHzの要素数以下である必要があります。

final int MAXBAND = 48;

//グローバル変数

Minim minim; //minimオブジェクト

AudioPlayer player; //演奏クラス

FFT fft; //FFT解析クラス

float specSize; //周波数分解幅

float initBand; //分解Hz

int stepCount; //表示するサンプリング単位幅

int wakuX, wakuY; //外枠の描画原点

int wakuWidth, wakuHeight; //外枠の幅と高さ

int barWidth; //棒グラフの幅

PImage back; //背景画像

//以下の48個のHz単位に棒グラフを描く

int bandHz[] = { 43, 43, 43, 43, 43, 43, 43, 43,

43, 43, 43, 43, 43, 43, 43, 43,

86, 86, 86, 86, 86, 86, 86, 86,

172, 172, 172, 172, 688, 688, 688, 688,

215, 215, 344, 344, 516, 516, 688, 688,

1032, 1032, 1204, 1376, 1548, 1720, 1892, 2064 };

void setup() {

size( 640, 480 );

//画面中央にスペクトルグラフを描画する

wakuX = 10;

wakuY = 10;

wakuWidth = 620;

wakuHeight = 460;

back = loadImage( "ensoukai.jpg" );

//音楽読み込み

minim = new Minim(this);

player = minim.loadFile("castle-the-order.mp3");

//FFT設定

fft = new FFT( player.bufferSize(), player.sampleRate());

//周波数分解幅を取得

//全周波数を、この数の個数に分割して分析可能。通常は513

specSize = fft.specSize();

//HANN窓指定。minimではHAMMINGより精度が高そう・・・

fft.window( FFT.HANN );

//初期分解Hz(getBandWidth)を求める

//分解幅1つ単位のHz。

//例えば分解Hzが 43 なら、43 × 513 = 22059Hzまで解析可能

initBand = fft.getBandWidth();

//棒グラフの幅

barWidth = wakuWidth / MAXBAND;

//音楽再生

player.play();

}

void draw() {

background( back );

//スペクトルを描画する範囲の外枠を描く

strokeWeight( 2 );

stroke( 0 );

noFill();

rect( wakuX, wakuY, wakuWidth, wakuHeight );

if( player.isPlaying() == false ){

return;

}

//FFT開始(左右混合分析)

//左のみなら player.left、右のみなら player.right を指定

fft.forward( player.mix );

int ToStep = 0; //ここから

int FromStep = 0; //ここまでの振幅を平均する

//スペクトルグラフ描画

for( int index = 0; index < MAXBAND; index++ ){

//指定されたHz単位の平均を採取するため

//計算範囲を求める

int bandStep = (int)( bandHz[index] / initBand );

if( bandStep < 1 ){ bandStep = 1; }

ToStep = ToStep + Math.round( bandStep );

if( ToStep > specSize ){ ToStep = (int)specSize; }

//平均値を計算

float bandAv = 0;

for( int j = FromStep ; j < ToStep; j++ ){

//振幅をDBに変換

float bandDB = 0;

if ( fft.getBand( j ) != 0 ) {

bandDB = 2 * ( 20 * ((float)Math.log10(fft.getBand(j))) + 40);

if( bandDB < 0 ){ bandDB = 0; }

}

bandAv = bandAv + bandDB;

}

bandAv = bandAv / bandStep; //平均値

FromStep = ToStep;

//グラフの描画座標を計算

float y = map( bandAv, 0, 250, 0, wakuHeight );

if( y < 0) { y = 0; }

//グラフの色を計算

color c1 = color( 0,0,255 );

color c2 = color( 255,255,0 );

color c3 = lerpColor( c1, c2, index/32.0 );

fill( c3, 140 );

//棒グラフを描画

rect( index*barWidth+wakuX,( wakuHeight-y )+wakuY, barWidth, y );

}

minim.loadFile（）で指定した音楽ファイルの周波数を分析し、スペクトラムアナライザを描画します。

44100Hzのサンプリングレートを持つ1024のバッファサイズの mp3 では、fft.getBandWidth()で得られる周波数分解幅は約43Hzです。上記サンプルは、これを前提に考えています。

また普通の音楽では高音域（10000Hz以上）の成分はあまり含まれていないため、低音から中音域を重点的にグラフ化するために、bandHz[] で指定したHz幅で棒グラフを描画しています。

分解したい幅と数は、お好みに合わせて調整してください。

＜出力サンプル＞

（画像URL:GAHAG | 著作権フリー写真・イラスト素材集様）

なお、上記サンプルプログラムの制作にあたり、下記サイト様を参照させて頂きました。ありがとうございます。

下記はサンプルプログラムと同じ動きになるように、 P5.js＋P5.sound で書き直したものです。

ブラウザ用にマウスクリックで分析（演奏）を開始し、再度クリックで停止するように改造してあります。動作イメージを確認できます。※

※ブラウザーによっては下記サンプルが表示されない事があります。IE11はNGでした。動作イメージを確認したい方は、FireFox、Chrome、Edgeなどでお試しください。

演奏される効果音は、wingless seraph 様から拝借しました。ありがとうございます。

PROCESSING逆引きリファレンス一覧へ戻る

本ページで利用しているアイコン画像は、下記サイト様より拝借しております。各画像の著作権は、それぞれのサイト様および作者にあります。

iconka.com 様
ICOOON MONO 様

◆PROCESSING 逆引きリファレンス

カテゴリー：音楽・演奏