◆PROCESSING 逆引きリファレンス
カテゴリー：ゲーム作成
多角形同士の当たり判定を行うには
【解説】
多くのゲームでは、物と物が衝突したかどうかを判定する処理（当たり判定）は定番ですね。
例えばシューティングゲームでは、敵と弾が衝突したかどうかを判定し、しかるべき処理を行います。
ゲーム専用のフレームワーク（UnityやCocos2d-X）では、専用の当たり判定命令が用意されています。
残念ながらPROCESSINGには、当たり判定を行う便利な標準命令はありません。
矩形同士、円同士の当たり判定については下記のページで解説しました。
では斜めになっている四角形同士（例えばひし形や、回転する四角形同士）や多角形の当たり判定は、どうしたら良いでしょうか？。
（画像URL:illust-AC 様：うーさん、kaeru-yaさん）
1つの方法として、回転する四角形や多角形同士は、図形の構成要素である各辺（線分）同士が交差しているかどうかを判定する事で、当たり判定を行うことが可能です。
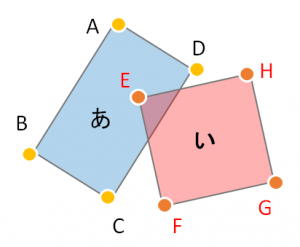
以下は回転している四角形同士の例です。頂点ABCDの四角形（あ)と、頂点EFGHの四角形（い)があります。この時、A-B、B-C、C-D、D-Aの各辺（線分）と、E-F、F-G、G-H、H-Eの各辺（線分）が1つでも交差していれば「当たっている」と考えます。
まずは、手始めに直線と線分の交差から考えます。
ある1点（x、y）を通過する傾きaの直線L（y=ax+b）をグラフで書くと下記のようになります。むか～し数学の時間に習いましたよね（笑）。
この時、グラフ上にある点P1、P2がグラフの左側（yより大きな側）にあるか、右側（yより小さい側）にあるかを考えます。以下の様な感じですね。
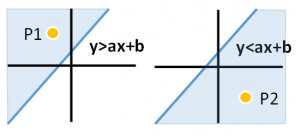上図のように、P1とP2がy軸を挟んで大小にわかれる場合、P1ーP2を結ぶ線分と直線は交差している事になります。
P1、P2が下図のように同じ側にあれば、P1ーP2を結ぶ線分と直線は交差しません。
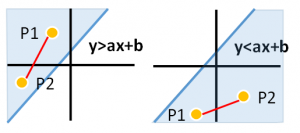2つの点（x1、y1）ー（x2、y2）を通る直線の方程式は以下のようになりますが
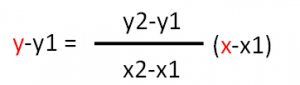
これを変形した以下の式に検査したい点P1、P2の座標を代入して、求まる結果の大小が同じ符号（正負）になるかどうかで（＝つまり y軸を挟んで同じ側にあるかどうかで）判定すれば、直線と線分が交差しているかどうかが判ります。
ただしansが0になる場合は、直線と点が重なっていると判定すべきです。
またこの式は直線と線分の交差判定になります。実際に行いたいのは線分同士の交差判定です。
よって例えば下図の場合では、CDを結ぶ仮直線LAと線分EFの交差判定を行い、かつEFを結ぶ仮直線LBと線分CDの交差判定を行って、ともに交差していると判定されるとき「当たり」となります。
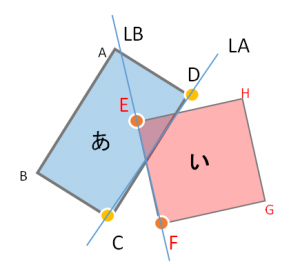
この方法を使うと四角形にかぎらず、多角形同士の衝突判定を行うことができるようになります。
※上記記事は フリー教材開発コミュニティFTEXT 様、Visual Basic Library 様の記事を参考とさせて頂きました。ありがとうございます。
例えば、傾いた四角形同士の当たり判定を行うには、傾いた四角形の四隅の点座標（ABCD、EFGH)を計算する必要があります。
傾いた四角形の四隅の点座標は、三角関数を使って計算可能です。
回転していない普通の四角形（あ）を考える時、この四角形が中央を基点にθ度だけ回転したのが、回転している四角形（い）です。
これは半径 r の円上にある点（P)がθ度だけ回転して作る点Qと同じことだとわかります。
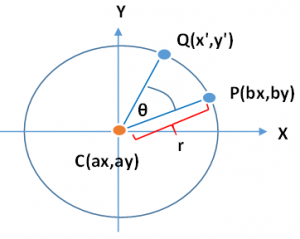
この点Pをθ度だけ回転させた位置にある点Qは、三角関数の「加法定理」により、以下の式で求めることが可能です。
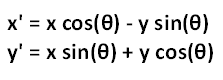これをPROCESSINGに適合した式に直すと、以下のようになります。
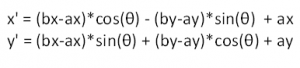※上記はKIT数学ナビゲーション 様、双流蒼天歌 様(2019/04 リンク不在)のページを参考とさせて頂きました。ありがとうございます。
【構文】
float c = cos( float angle );
float s = sin( float angle );
【パラメータ】
c ： 得られたコサイン値
s ： 得られたサイン値
angle ： 角度（ラジアン）
【注意】
ぞれぞれの三角関数に与える角度は「度」ではなく「ラジアン」です。度からラジアンへの変換は、radians()命令で行えます。
またこれらの関数は、時計回りの角度を扱います。私達が普段数学などで使う角度は反時計回りのことが多いと思いますので、注意してください。
反時計回りで計算したい場合は、負の値を与える必要があります。
【関連記事】
サンプルプログラム
非矩形な四角形の衝突判定例：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 |
//座標管理用クラス class Point { int x; int y; //コンストラクタ Point( int ix, int iy ){ x = ix; y = iy; } } Point[] whiteRect = new Point[4]; Point[] blueRect = new Point[4]; //初期化関数 void setup(){ size(400,400); //四角形の座標を作成する whiteRect[0] = new Point( 145, 120 ); //A whiteRect[1] = new Point( 150, 180 ); //B whiteRect[2] = new Point( 190, 240 ); //C whiteRect[3] = new Point( 240, 150 ); //D blueRect[0] = new Point( 190, 170 ); //E blueRect[1] = new Point( 230, 240 ); //F blueRect[2] = new Point( 260, 260 ); //G blueRect[3] = new Point( 290, 180 ); //H textSize(24); textAlign(LEFT,BOTTOM); } //描画処理関数 void draw(){ background( 0 ); //白い四角形を描く fill(255,255,255); text( "A", whiteRect[0].x-10, whiteRect[0].y-5); text( "B", whiteRect[1].x-30, whiteRect[1].y+10); text( "C", whiteRect[2].x-20, whiteRect[2].y+30); text( "D", whiteRect[3].x, whiteRect[3].y-5); dispRect( whiteRect, color(255,255,255) ); //青い四角形を描く fill( 50,50,255 ); text( "E", blueRect[0].x-20, blueRect[0].y); text( "F", blueRect[1].x-20, blueRect[1].y+30); text( "G", blueRect[2].x+10, blueRect[2].y+25); text( "H", blueRect[3].x+10, blueRect[3].y); dispRect( blueRect, color(50,50,255) ); //衝突判定 //直線CDと辺EFを判定する boolean r1 = isCollisionSide( whiteRect[2], whiteRect[3], blueRect[0], blueRect[1] ); //直線EFと辺CDを判定する boolean r2 = isCollisionSide( blueRect[0], blueRect[1], whiteRect[2], whiteRect[3] ); //両方ともクロスしていれば当たり println( "r1=" + r1 + "/r2=" + r2 ); if( r1 == true && r2 == true ) print("当たりです"); noLoop(); } //四角を描く関数 void dispRect( Point[] r, int c ){ strokeWeight(2); stroke(c); line( r[0].x, r[0].y, r[1].x, r[1].y); line( r[1].x, r[1].y, r[2].x, r[2].y); line( r[2].x, r[2].y, r[3].x, r[3].y); line( r[3].x, r[3].y, r[0].x, r[0].y); } //-------------------------------------------- //衝突判定関数 //直線 r1-r2と、辺p1-p2がクロスするか判定する //-------------------------------------------- boolean isCollisionSide( Point r1, Point r2, Point p1, Point p2 ){ float t1, t2; //判定する辺を目立たせる処理（衝突判定とは関係なし） strokeWeight(4); stroke(color(255,0,0)); line( r1.x, r1.y, r2.x, r2.y); line( p1.x, p1.y, p2.x, p2.y); //衝突判定計算 t1 = (r1.x-r2.x)*(p1.y-r1.y)+(r1.y-r2.y)*(r1.x-p1.x); t2 = (r1.x-r2.x)*(p2.y-r1.y)+(r1.y-r2.y)*(r1.x-p2.x); //それぞれの正負が異なる（積が負になる）か、0（点が直線上にある） //ならクロスしている if( t1*t2 < 0 || t1 == 0 || t2 == 0 ){ return( true ); //クロスしている } else { return( false ); //クロスしない } } |
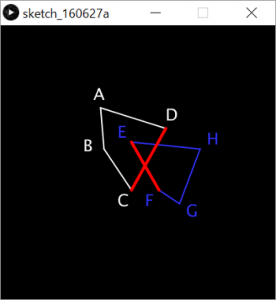
上記を実行すると白い四角形（ABCD)と青い四角形（EFGH)を描画し、白い四角形の辺CDと、青い四角形の辺EFが重なっているかどうかを判定します。
isCollisionSide() が当たり判定を行っている関数です。CDを仮直線と見立てて辺EFとのクロスを判定する処理（r1）と、EFを仮直線と見立てて辺CDとのクロスを判定する処理（r2）がある事に注目してください。
どの辺同士を判定しているか目立たせるために、isCollisionSide() の中で判定対象の辺を赤く描画していますが、この処理は判定処理とは直接関係がありません。
＜出力サンプル＞
加法定理で四角形を回転させる例：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
//点管理用クラス class Point { float x; float y; Point( float ix, float iy ){ x = ix; y = iy; } } //四角形管理用クラス class myRect { Point[] rp; //四隅の座標 Point cp; //中央座標 //左上座標p、幅w、高さh myRect( Point p, int w, int h ){ rp = new Point[4]; rp[0] = new Point( p.x, p.y ); rp[1] = new Point( p.x + w, p.y ); rp[2] = new Point( p.x + w ,p.y + h ); rp[3] = new Point( p.x, p.y + h ); cp = new Point( p.x + w/2, p.y + h/2 ); } } myRect rct; //元四角形 float deg; //角度 int rectW, rectH; //元四角形の幅と高さ /************************************************** * 加法定理回転座標計算関数 *------------------------------------------------- * 回転する点座標 p1 * 回転中央座標 cp * 回転角度 deg ***************************************************/ Point caclRotate( Point p1, Point cp, float deg ){ float cx, cy; cx = (cp.x-p1.x)*cos(radians(deg))-(cp.y-p1.y)*sin(radians(deg))+ cp.x; cy = (cp.x-p1.x)*sin(radians(deg))+(cp.y-p1.y)*cos(radians(deg))+ cp.y; return( new Point( cx, cy )); } //初期処理関数 void setup(){ size(300,300); rectW = 150; //元四角形の幅 rectH = 50; //元四角形の高さ //元四角形を作成する rct = new myRect( new Point( 80,110), rectW, rectH ); deg = 0; } //描画処理関数 void draw(){ background( 0 ); //元の四角形を白で描く noFill(); stroke( 255 ); strokeWeight(4); rect( rct.rp[0].x, rct.rp[0].y, rectW, rectH ); //回転させた四角形の四隅座標を計算する Point rp0, rp1, rp2, rp3; rp0 = caclRotate( rct.rp[0], rct.cp, deg ) ; rp1 = caclRotate( rct.rp[1], rct.cp, deg ) ; rp2 = caclRotate( rct.rp[2], rct.cp, deg ) ; rp3 = caclRotate( rct.rp[3], rct.cp, deg ) ; //回転させた四角形を青で描く stroke( color( 50,50,255) ); line( rp0.x, rp0.y, rp1.x, rp1.y ); line( rp1.x, rp1.y, rp2.x, rp2.y ); line( rp2.x, rp2.y, rp3.x, rp3.y ); line( rp3.x, rp3.y, rp0.x, rp0.y ); deg++; if( deg > 359 ) deg = 0; } |
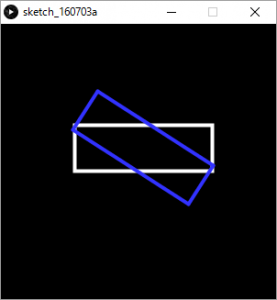
上記を実行すると、画面中央に描かれる白い四角形が、時計回りに回転した青い四角形が描かれます。
caclRotate() が加法定理により座標を回転させている処理です。
＜出力サンプル＞
回転する四角形同士の衝突判定例：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 |
//点管理用クラス class Point { float x; float y; //コンストラクタ Point( float ix, float iy ){ x = ix; y = iy; } //点移動関数 void addPoint( int add ){ x = x + add; y = y + add; } } //四角形管理用クラス class myRect { Point[] rp; //四隅の座標 Point cp; //中央座標 //コンストラクタ //左上座標p、幅w、高さh myRect( Point p, int iw, int ih ){ rp = new Point[4]; rp[0] = new Point( p.x, p.y ); rp[1] = new Point( p.x + iw, p.y ); rp[2] = new Point( p.x + iw , p.y + ih ); rp[3] = new Point( p.x, p.y + ih ); cp = new Point( p.x + iw/2, p.y + ih/2 ); } //中心点を移動する関数 void moveCenter(int move ){ cp.addPoint( move ); for( int i = 0; i < 4; i++ ){ rp[i].addPoint( move ); } } //四角形を描画する関数 void dispRect( int c ){ stroke( c ); strokeWeight( 4 ); line( rp[0].x, rp[0].y, rp[1].x, rp[1].y ); line( rp[1].x, rp[1].y, rp[2].x, rp[2].y ); line( rp[2].x, rp[2].y, rp[3].x, rp[3].y ); line( rp[3].x, rp[3].y, rp[0].x, rp[0].y ); } //四角形を deg度回転させる関数 void rotate( float deg ){ rp[0] = caclRotate( rp[0], cp, deg ); rp[1] = caclRotate( rp[1], cp, deg ); rp[2] = caclRotate( rp[2], cp, deg ); rp[3] = caclRotate( rp[3], cp, deg ); } /************************************************** * 加法定理回転座標計算関数 *------------------------------------------------- * 回転する点座標 p1 * 回転中央座標 cp * 回転角度 deg ***************************************************/ Point caclRotate( Point p1, Point cp, float deg ){ float cx, cy; cx=(cp.x-p1.x)*cos(radians(deg))-(cp.y-p1.y)*sin(radians(deg))+ cp.x; cy=(cp.x-p1.x)*sin(radians(deg))+(cp.y-p1.y)*cos(radians(deg))+ cp.y; return( new Point( cx, cy )); } } /************************************************** * 衝突判定関数 *------------------------------------------------- * 直線 r1-r2と、辺p1-p2がクロスするか判定する * クロスする場合は true. しない場合は false. ***************************************************/ boolean isCollisionSide( Point r1, Point r2, Point p1, Point p2 ){ float t1, t2; //2点r1-r2を通る直線に対し、p1、p2がどの位置にあるか計算する t1 = (r1.x-r2.x)*(p1.y-r1.y)+(r1.y-r2.y)*(r1.x-p1.x); t2 = (r1.x-r2.x)*(p2.y-r1.y)+(r1.y-r2.y)*(r1.x-p2.x); //それぞれの正負が異なる（積が負になる）か、0（点が直線上にある） //ならクロスしている if( t1*t2 < 0 || t1 == 0 || t2 == 0 ){ return( true ); //クロスしている } else { return( false ); //クロスしない } } //グローバル変数 myRect rectWhite; //白四角形 myRect rectBlue; //青四角形 int rw, rh; //四角形の幅と高さ int moveW, moveB; //四角形の移動量 float deg; //回転角度 int c1, c2; //描画色 //初期処理関数 void setup(){ size(300,300); rw = 100; //四角形の幅 rh = 50; //四角形の高さ moveW = 2; //白四角は下に移動 moveB = -2; //青四角は上に移動 //四角形を作成する rectWhite = new myRect( new Point(0,0), rw, rh ); rectBlue = new myRect( new Point(width - rw,height - rh), rw, rh ); deg = 2; frameRate(30); } //描画処理関数 void draw(){ background( 0 ); //四角形の色を作成する c1 = color(255,255,255); //白 c2 = color(50,50,255); //青 //中心を移動する rectWhite.moveCenter( moveW ); rectBlue.moveCenter( moveB ); //画面の端にきたら反転する if( rectWhite.cp.x < 0 || rectWhite.cp.x > width || rectWhite.cp.y < 0 || rectWhite.cp.y > height ){ moveW = moveW * -1; } if( rectBlue.cp.x < 0 || rectBlue.cp.x > width || rectBlue.cp.y < 0 || rectBlue.cp.y > height ){ moveB = moveB * -1; } //回転させた四角形の四隅座標を計算する rectWhite.rotate( deg ); rectBlue.rotate( -deg ); //衝突判定を行う //白四角辺 [0]-[1] と青四角辺[0]-[1]、[1]-[2]、[2]-[3]、[3]-[0] //白四角辺 [1]-[2] と青四角辺[0]-[1]、[1]-[2]、[2]-[3]、[3]-[0] //白四角辺 [2]-[3] と青四角辺[0]-[1]、[1]-[2]、[2]-[3]、[3]-[0] //白四角辺 [3]-[0] と青四角辺[0]-[1]、[1]-[2]、[2]-[3]、[3]-[0] //をクロス判定する boolean t1, t2; //i は白四角の4辺のインデックス for( int i = 0; i < 4; i++ ){ //座標配列が3-4の比較なら、3-0の比較に置き換える int toi; toi = i + 1; if( toi > 3 ) toi = 0; //j は青四角の4辺のインデックス for( int j = 0; j < 4; j++ ){ //座標配列が3-4の比較なら、3-0の比較に置き換える int toj; toj = j + 1; if( toj > 3 ) toj = 0; //クロス判定 t1 = isCollisionSide( rectWhite.rp[i], rectWhite.rp[toi], rectBlue.rp[j], rectBlue.rp[toj] ); t2 = isCollisionSide( rectBlue.rp[j], rectBlue.rp[toj], rectWhite.rp[i], rectWhite.rp[toi] ); if( t1 == true && t2 == true ){ //クロスしているので赤色にする c1 = color( 255,100,100); c2 = c1; break; } } } //描画する rectWhite.dispRect( c1 ); rectBlue.dispRect( c2 ); } |
上記を実行すると、白い四角形と青い四角形が回転しながら移動し、衝突します。
衝突している間、四角形が赤く描かれます。
回転する四角形の辺同士が重なっているかどうかを判定しているのがisCollisionSide()関数です。
回転する四角形の四隅の座標は加法定理により、caclRotate()関数で計算しています。
＜出力サンプル＞
下記はサンプルプログラムをP5.jsで書き直したものです。動作イメージを確認できます。
本ページで利用しているアイコン画像は、下記サイト様より拝借しております。各画像の著作権は、それぞれのサイト様および作者にあります。