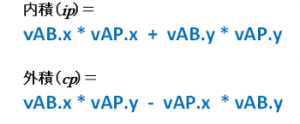◆PROCESSING 逆引きリファレンス
カテゴリー：ゲーム作成
円と線分の当たり判定を行うには
【解説】
多くのゲームでは、物と物が衝突したかどうかを判定する処理（当たり判定）は定番ですね。
ゲーム専用のフレームワーク（UnityやCocos2d-X）では、専用の当たり判定命令が用意されています。
残念ながらPROCESSINGには、当たり判定を行う便利な標準命令はありません。
矩形同士、円同士、多角形同士の当たり判定については下記のページで解説しました。
ここでは斜めになっている四角形と円の当たりを判定を考えてみます。
四角形と円の当たりを判定は、例えば四角形のミサイルと円状のUFOや、ボール反射ゲームの反射バーと球の当たり判定などで利用できそうですね。
（画像URL：deviantart.com 様、GAHAG | 著作権フリー写真・イラスト素材集 様：著作者（Free Download Web さん/ID：201411190600）、pixabay 様：OpenClipart-Vectorsさん）
なんだか難しそうですが、要は四角形の辺を構成している線分と円の中心点を用いて、「線分と中心点の最短距離」を求め、その距離が円の半径よりも大きいか小さいかを判定すればOKです。
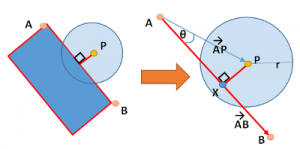
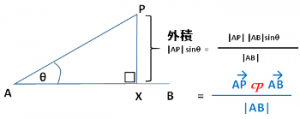
上図の場合、青い四角形と円があたっているかどうかは、四角形の辺ABに向かって円の中心点Pから引いた垂線PXの長さが、半径rよりも大きいか小さいかを判定すれば良いことがわかります。
ある点Pから線分ABへ下ろした垂線PXの長さを知るには、ベクトル演算の外積を使います。
また点Xの座標を知るにはAXの長さを得る必要がありますが、この時はベクトル演算の内積を使います。
もう・・・ベクトル演算なんてとうの昔に忘れ去りましたので・・・いまさらオジサマに内積と外積の説明はできません（汗）が・・・単純に書くと下図のような関係になります。
●AXの長さ（内積を使う）
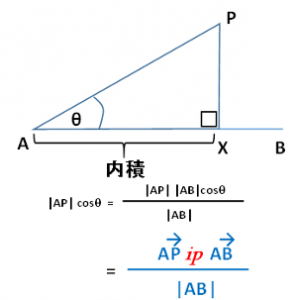
ベクトルAPの長さ（|AP|）×コサインθが内積（ベクトルAXの長さ）です。
●PXの長さ（外積を使う）
ベクトルAPの長さ（|AP|）×サインθが外積（ベクトルPXの長さ）です。
サイン・コサインを使って計算しても良いのですが、点A、B、Pの座標がわかっているのであれば、単純な掛け算で計算可能です。
上図の場合、内積の式は以下の様に変換できます。
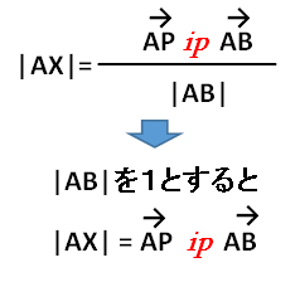
ip は「内積（inner product）」の事です。ここでのポイントはベクトルABの長さ（|AB|）を1と見立てて、計算を単純化している事です。
また外積の式は以下の様に変換できます。
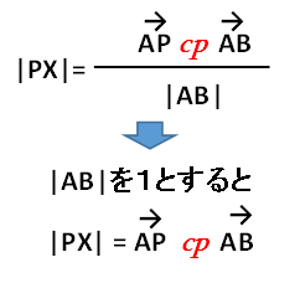
cpは「外積（cross product）」の事です。
このように長さを1に見立てたベクトルの事を「単位ベクトル」と呼び、あるベクトルを単位ベクトルに変換する事を「正規化（ノーマライズ）」と呼びます。
最終的にプログラムで計算する際には、ベクトルABを正規化したものをvAB、ベクトルAPをvAPとすると、以下の計算式で求めることが可能です。
※上記記事は、deq notes 様、2D当たり判定超入門 様、ゲームプログラミング技術集 様を参考とさせて頂きました。ありがとうございます。
線分と円の当たり判定を考える際、もう1つ考慮しなければいけない事があります。それは線分の範囲内に円の中心があるか否かという事です。
例えば下図の場合
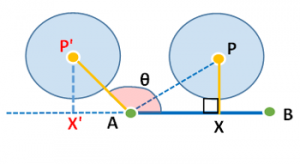
点 P’ はベクトルABの外（点Aよりも左）にあります。この場合、点P’ と線分ABの最短距離はX’P’ ではなくてAP’ になります。点Pが線分AB上にあれば、XP が最短距離です。
それでは点Pが線分ABから見てどこにあるのかを、どうやって判定すれば良いでしょうか？。
これにはベクトルABとベクトルAPが作る角度（θ）のコサイン値が正負のどちらであるかを判定すれば良いと、いろいろなサイト様に解説されています。
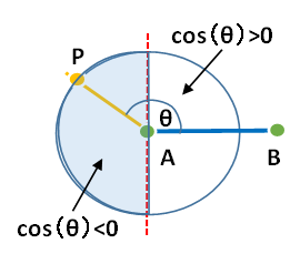
これは簡単にいえば、点Aから見て点Xの方向が右か左か（AXの長さが正か負か）を判断すれば良いという事です。
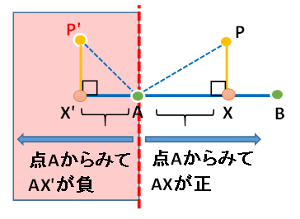AXの方向（長さ）については、先に説明した内積の計算で求めることが可能です。
また以下の様なケースもあります。
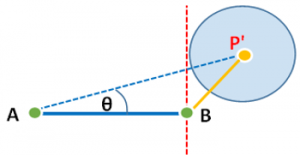
点P’ が点Bよりも右側にある場合です。この場合も線分ABと点P’の最短距離は、BP’となります。
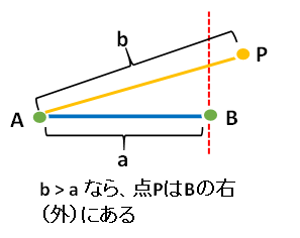
この場合は、ABの長さ（a）を内積計算で求めて、APの長さ（b）と比べてどちらが長い（大きい）かを判断すれば良い事になります。bの方が長ければ、点Pは点Bの右側にあります。
※上記はGihyo.jp 様：ActionScript 3.0で始めるオブジェクト指向スクリプティング記事を参考とさせて頂きました。ありがとうございます。
下図のような三角形APXにおいて
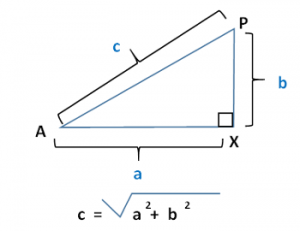
ベクトルAPの長さ（辺cの長さ）は三平方の定理により計算可能ですが、PROCESSINGには2点間の長さを計算してくれる便利な命令 dist() があります。
今回はこれを使ってみたいと思います。
【構文】
float 2df = dist( float x1, float y1, float x2, float y2 ) ;
float 3df = dist( float x1, float y1, float z1, float x2, flost y2, float z2 ) ;
【パラメータ】
2df ： 計算された ( x1, y1 ) – ( x2, y2 ) の距離
3df ： 計算された ( x1, y1, z1 ) – ( x2, y2, z2 ) の距離
x1、y1、z1 ： 1つ目の座標
x2、y2、z2 ： 2つ目の座標
Zを用いる計算は size() で P3D の3D系座標を指定している場合に限ります。
【関連記事】
サンプルプログラム
2点間の距離を計算する例：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 |
//----------------------- //点管理クラス //----------------------- class Point2D { float x; //横位置 float y; //縦位置 //コンストラクタ Point2D( float ix, float iy ){ x = ix; y = iy; } //描画処理 void disp( color c ){ stroke( c ); strokeWeight( diaP ); point( x, y ); } } //各変数 Point2D pointA, pointB; float len; float diaP; //端点の円の直径 void setup(){ size(300,300); //各座標生成 pointA = new Point2D( 20, 20 ); pointB = new Point2D( 280, 280 ); diaP = 20; } void draw(){ background(255); noFill(); //塗りつぶしなし stroke( 0 ); //線の色は黒 strokeWeight( 2 ); //幅は2 //直線を描く line( pointA.x, pointA.y, pointB.x, pointB.y ); pointA.disp( color( 0,0,255 ) ); pointB.disp( color( 0,255,0 ) ); //AB間の距離を求めて表示する fill(0); len = dist( pointA.x, pointA.y, pointB.x, pointB.y ); textSize(24); text( len, 24, 24 ); } void mouseDragged(){ //点Aがドラッグされたか判定する float plen = dist(mouseX, mouseY, pointA.x, pointA.y) ; if( plen < diaP/2 ){ pointA.x = mouseX; pointA.y = mouseY; } else { //点Bがドラッグされたか判定する plen = dist(mouseX, mouseY, pointB.x, pointB.y) ; if( plen < diaP/2 ){ pointB.x = mouseX; pointB.y = mouseY; } } } |
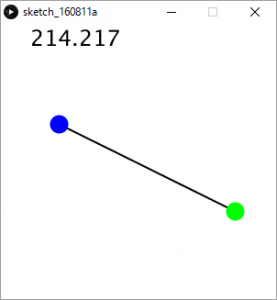
上記プログラムを実行すると青点（A)と緑点（B)を結ぶ直線が描かれます。また画面左上にAB間の長さが表示されます。
マウスで点Aまたは点Bをドラッグして動かすと、距離表示が変わることがわかると思います。
＜出力サンプル＞
円と線分の衝突判定例：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 |
//----------------------- //点管理クラス //----------------------- class Point2D { float x; //横位置 float y; //縦位置 //コンストラクタ Point2D( float ix, float iy ){ x = ix; y = iy; } //描画処理 void disp( color c ){ stroke( c ); strokeWeight( diaP ); point( x, y ); } } //----------------------- //ベクトル管理クラス //----------------------- class Vector2D { float x; //横成分 float y; //縦成分 float len; //コンストラクタ Vector2D(){ x = 0; y = 0; } //オーバロード Vector2D( Point2D A, Point2D B ){ x = B.x - A.x; y = B.y - A.y; //長さを計算 len = dist(A.x, A.y, B.x, B.y ); } //単位ベクトル生成 Vector2D normalVec( ){ Vector2D retV = new Vector2D(); retV.x = x / len; retV.y = y / len; return( retV ); } //ベクトル内積計算 float inner( Vector2D v1 ) { return ( x * v1.x + y * v1.y ); } //ベクトル外積計算 float cross( Vector2D v1 ) { return( x * v1.y - v1.x * y ); } } //各変数 Point2D pointA, pointB, pointP, pointX; float diaC; //中央円の直径 float diaP; //端点の円の直径 Vector2D vecAB, vecAP, vecBP; void setup(){ size(300,300); //各座標生成 pointA = new Point2D( 40, 40 ); pointB = new Point2D( 260, 260 ); pointP = new Point2D( 150, 150 ); diaC = 100; diaP = 20; } void draw(){ background(255); noFill(); //塗りつぶしなし //直線を描く stroke( 0 ); //線の色は黒 strokeWeight( 2 ); //幅は2 line( pointA.x, pointA.y, pointB.x, pointB.y ); pointA.disp( color( 0,0,255 ) ); pointB.disp( color( 0,255,0 ) ); //当たり判定 boolean ret = isCollisionLineCircle( ); if( ret == true ) { //HITしたので円を赤くし、最短距離にある点Xを描く stroke( color(255,0,0) ); pointX.disp( color( 100,100,255 )); } else { //円は黒色 stroke( 0 ); } //中央の円を描画する strokeWeight( 2 ); //幅は2 ellipse( pointP.x, pointP.y, diaC, diaC ); } //----------------------- //当たり判定 //----------------------- boolean isCollisionLineCircle( ){ //ベクトルを生成 vecAB = new Vector2D( pointA, pointB ); vecAP = new Vector2D( pointA, pointP ); vecBP = new Vector2D( pointB, pointP ); //ABの単位ベクトルを計算 Vector2D normalAB = vecAB.normalVec( ); //AからXまでの距離を //単位ベクトルABとベクトルAPの内積で求める float lenAX = normalAB.inner( vecAP ); float shortestDistance; //線分APとPの最短距離 if( lenAX < 0 ){ //AXが負なら APが円の中心までの最短距離 shortestDistance = vecAP.len; } else if( lenAX > vecAB.len ){ //AXがAPよりも長い場合は、BPが円の中心 //までの最短距離 shortestDistance = vecBP.len; } else { //PがAB上にあるので、PXが最短距離 //単位ベクトルABとベクトルAPの外積で求める shortestDistance = abs( normalAB.cross( vecAP )); } //Xの座標を求める(AXの長さより計算） pointX = new Point2D( pointA.x + ( normalAB.x * lenAX ), pointA.y + ( normalAB.y * lenAX ) ); boolean hit = false; if( shortestDistance < diaC/2 ) { //最短距離が円の半径よりも小さい場合は、当たり hit = true; } return( hit ); } void mouseDragged(){ //点Aがドラッグされたか判定する float plen = dist(mouseX, mouseY, pointA.x, pointA.y) ; if( plen < diaP/2 ){ pointA.x = mouseX; pointA.y = mouseY; } else { //点Bがドラッグされたか判定する plen = dist(mouseX, mouseY, pointB.x, pointB.y) ; if( plen < diaP/2 ){ pointB.x = mouseX; pointB.y = mouseY; } } } |
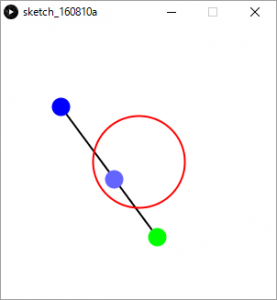
上記プログラムを実行すると青点（A)と緑点（B)を結ぶ直線が描かれます。また画面中央に円が描かれます。
マウスで青点または緑点をドラッグし、線分が円と重なると、円が赤くなります。
Point2Dは点の座標を管理するクラス、Vector2Dはベクトルを管理するクラスです。
Vector2Dクラスには、本文で説明した正規化、内積、外積を計算するメソッドが備わっています。
正規化を計算する都合上、（無理やり）オーバロードコンストラクタを使っていますが、線分と円の当たり判定には直接関係ありません。
オーバロードコンストラクタの利用は、私の力量不足ですね・・・。この辺りは、もう少しスマートな記述があるかもしれません（汗）。
＜出力サンプル＞
下記はサンプルプログラムをP5.jsで書き直したものです。マウス（またはタッチ操作）で、青い点か緑の点をドラッグしてください。動作イメージを確認できます。
本ページで利用しているアイコン画像は、下記サイト様より拝借しております。各画像の著作権は、それぞれのサイト様および作者にあります。