◆PROCESSING 逆引きリファレンス
 カテゴリー:演算処理
カテゴリー:演算処理
sin/cos/tanを計算するには
【解説】
三角関数は、機械加工や測量、土木工学などの分野に携わる人にとっては現実の仕事で利用する機会があるようですが、普通のサラリーマンをしているだけだと、なかなか使う機会がありません。
一方でゲームプログラミングを行うと、意外と使う機会があります。
ゲームプログラミングが趣味なオジサマは、「こんなに使うのなら、もっとちゃんと勉強しておけばよかった・・・」と反省しまくりです(汗)。
多くのプログラミング言語がそうであるように、PROCESSINGにもサイン、コサイン、タンジェントを計算する便利な命令があります。
【構文】
float s = sin( angle ) ;
float c = cos( angle ) ;
float t = tan( angle );
【パラメータ】
s:サイン値
c:コサイン値
t:タンジェント値
angle:角度(ラジアン)
【注意】
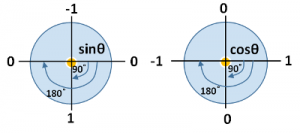
与える角度は時計回りのラジアンです。私達が数学でよく目にする反時計回りの角度ではありません。
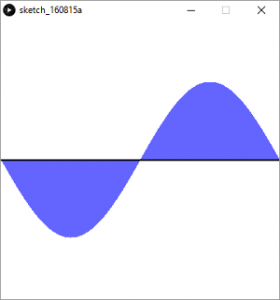
sinは0度の時0、90度で1、180度で0、270度で-1、360度で0となる-1から1までの範囲の数値です。
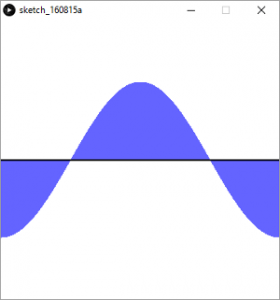
cosは0度の時1、90度で0、180度で-1、270度で0、360度で1となる-1から1までの範囲の数値です。
tanは0度の時0、90度でプラス無限大、180度で0、270度でマイナス無限大、360度で0の範囲をとる数値です。
ただしPROCESSINGでは計算誤差がでるため、角度によっては理論通りの値にはなりません。例えば sin( 180 ) は理論的には0ですが 0.00000008742278 といった0に限りなく近い値になります。
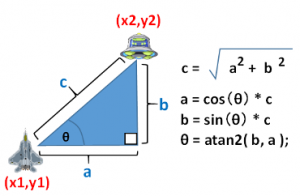
ゲームプログラミングに限った話ですが、タンジェントはそのまま使うのではなくて、アークタンジェント(atanまたはatan2)として利用し、目標までの角度を知るのに使うことが多いようです。
 (画像URL:deviantart.com 様、GAHAG | 著作権フリー写真・イラスト素材集 様:著作者(Free Download Web さん/ID:201411190600))
(画像URL:deviantart.com 様、GAHAG | 著作権フリー写真・イラスト素材集 様:著作者(Free Download Web さん/ID:201411190600))
上図にゲームでよく使う三角関数と三平方の定理の関係をまとめました。
アークタンジェントについては「追尾ミサイルを打つには」で解説しています。
sin/cos/tanの各命令は、360度よりも大きな角度、あるいは0度よりも小さな負の角度を与えた場合でもエラーにはなりません。この辺はプログラマー側で注意する必要があります。
【関連記事】
サンプルプログラム
sinカーブを描く例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
void setup(){ size(360,360); } void draw(){ background(255); //青線の準備 stroke(color(100,100,255)); float x = 0; //0度から360度のsinカーブを描く for( int deg = 0; deg < 361; deg++){ //線は基準線から上下100ピクセル幅で引く float y = sin( radians( deg ) ) * 100 + height/2; line( x, height/2, x, y ); x = x + 1; } //中央に黒い基準線を引く strokeWeight( 2 ); stroke(0); line( 0,height/2, width, height/2 ); noLoop(); } |
画面中央から上下方向に向かって、青線でサインカーブを描きます。
degが角度です。degが0度から180度の間 sin()は正の値を返すため、線は下方向に伸びます。180度から360度では負の値を返すため、線は上方向に伸びます。
cosカーブを描く例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
void setup(){ size(360,360); } void draw(){ background(255); //青線の準備 stroke(color(100,100,255)); float x = 0; //0度から360度のcosカーブを描く for( int deg = 0; deg < 361; deg++){ //線は基準線から上下100ピクセル幅で引く float y = cos( radians( deg ) ) * 100 + height/2; line( x, height/2, x, y ); x = x + 1; } //中央に黒い基準線を引く strokeWeight( 2 ); stroke(0); line( 0,height/2, width, height/2 ); noLoop(); } |
前述のサンプルプログラムでsin() と書かれていた箇所をcos()に変えただけです。
画面中央から上下方向に向かって、青線でコサインカーブを描きます。
degが角度です。degが0度から90度の間 cos()は正の値を返すため、線は下方向に伸びます。90度から270度では負の値を返すため、線は上方向に伸びます。
そして270度から360度では再び正の値を返すため、線は下方向に伸びます。
tanカーブを描く例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
void setup(){ size(360,360); } void draw(){ background(255); //青線の準備 stroke(color(100,100,255)); float x = 0; //0度から360度のtanカーブを描く for( int deg = 0; deg < 361; deg++){ //線は基準線から上下100ピクセル幅で引く float y = tan( radians( deg ) ) * 100 + height/2; line( x, height/2, x, y ); x = x + 1; } //中央に黒い基準線を引く strokeWeight( 2 ); stroke(0); line( 0,height/2, width, height/2 ); noLoop(); } |
同じくタンジェントカーブの例です。
sinカーブで絵を動かす例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
PImage fighter; //戦闘機 int deg; //角度 int x; //横位置 void setup(){ size(360,360); fighter = loadImage("X02C.png"); imageMode(CENTER); deg = 0; x = width; //右端から開始 } void draw(){ background(255); //戦闘機をsinカーブで動かす float y = sin( radians( deg ) ) * 100 + height/2; image( fighter, x, y ); deg++; x--; //画面端に達したら最初から繰り返し if( x < -fighter.width ){ x = width; deg = 0; } } |
単純なカーブを描くだけだと面白くありませんので(汗)、シューティングゲームでよく登場するような動きのあるサンプルを掲載しました。
実行すると右端から戦闘機がサインカーブを描きながら移動します。
<出力サンプル>
(画像URL:deviantart.com 様)
円運動させる例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
float deg; //回転角度 float rad; //回転半径 int ex, ey; //地球を描く場所 PImage earth, gosat, cosmos; void setup(){ size(300,300); earth = loadImage( "earth.png" ); gosat = loadImage( "gosat.png" ); cosmos = loadImage( "cosmos.png" ); //初期化。地球は画面中央に配置 imageMode( CENTER ); ex = width/2; ey = height/2; deg = 0; rad = 100; } void draw(){ background( cosmos ); //地球を中央に描画 image( earth, ex, ey ); //衛星の座標を計算して描画 float sx, sy; sx = cos( radians( deg ) ) * rad + ex; sy = sin( radians( deg ) ) * rad + ey; image( gosat, sx, sy ); //次の角度を求める deg++; if( deg > 360 ) deg = 0; } |
上記を実行すると、地球のまわりを人工衛星が周回します。人工衛星の座標をsin()とcos()で求めています。
<出力サンプル>
 (画像URL:GAHAG | 著作権フリー写真・イラスト素材集 様:ID:201404190200、JAXSA 様:GOSAT、宇宙物理2chまとめ 様)
(画像URL:GAHAG | 著作権フリー写真・イラスト素材集 様:ID:201404190200、JAXSA 様:GOSAT、宇宙物理2chまとめ 様)
下記はサンプルプログラムをP5.jsで書き直したものです。動作イメージを確認できます。
本ページで利用しているアイコン画像は、下記サイト様より拝借しております。各画像の著作権は、それぞれのサイト様および作者にあります。