◆PROCESSING 逆引きリファレンス
 カテゴリー:ゲーム作成
カテゴリー:ゲーム作成
矩形同士の当たり判定を行うには
【解説】
多くのゲームでは、物と物が衝突したかどうかを判定する処理(当たり判定)は定番ですね。
例えばシューティングゲームでは、敵と弾が衝突したかどうかを判定し、しかるべき処理を行います。
ゲーム専用のフレームワーク(UnityやCocos2d-X)では、専用の当たり判定命令が用意されています。
残念ながらPROCESSINGには、当たり判定を行う便利な標準命令はありません。
無いものは作るしかないというわけで(笑)、ここでは画面上に登場するキャラクターを囲む四角形を用いて、矩形同士の当たり判定を行う方法について解説したいと思います。
長方形(四隅の角がすべて90度のもの)を矩形(くけい)と呼びます。以下はすべて矩形です。
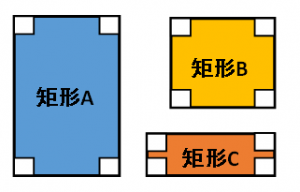
以下は矩形とは呼びません(笑)。
矩形同士が接触している(当たっている)とは、たとえば以下の様な状態を指します。
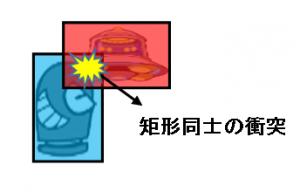 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
青い矩形と赤い矩形が接触しています。これを判定するには、おおまかに2つの方法があります。
- その1:矩形の原点と対角座標を使って判定する
- その2:矩形の中心座標と幅・高さを使って判定する
※以下の記事は●▲▼●ブログ 様の記事を参考とさせて頂きました。特に「その2」の判定方法(無欲な壺 様のコメント)は目からウロコでした。ありがとうございました。
●その1:矩形の原点と対角座標を使って判定する
PROCESSINGの矩形は、初期状態では左上隅を原点として、幅(w)と高さ(h)を持つ四角形で表すことが可能です。以下の様な感じです。
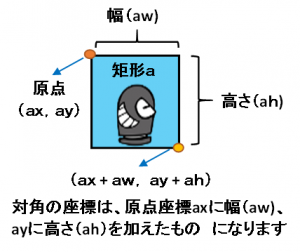 (画像URL:illust-AC 様:うーさん)
(画像URL:illust-AC 様:うーさん)
赤い矩形(矩形b)も同じように表すことができます。
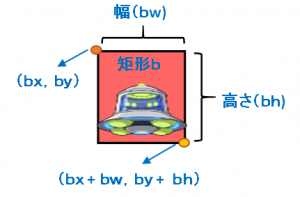 (画像URL:illust-AC 様:kaeru-yaさん)
(画像URL:illust-AC 様:kaeru-yaさん)
この原点座標と矩形の幅・高さを使って、2つの矩形の衝突を判定します。判定する際には、横方向(x)と縦方向(y)を別々に考えます。
まず横方向に着目すると、当たっている条件は以下であることがわかります。
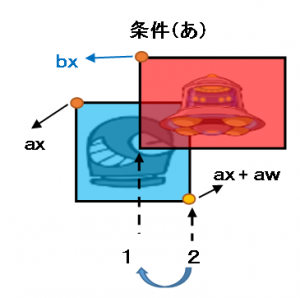
◆条件あ
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
文章で書くと、矩形aの対角(ax + aw:2番の位置)からみて、矩形bの原点(bx:1番の位置)が左にある(小さい)事です。式にすると bx < ( ax + aw ) が成り立つ時。これを「条件あ」とします。
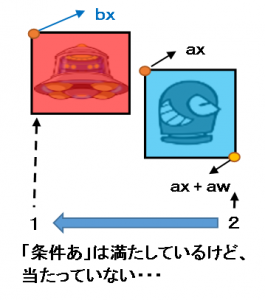
でも次のような場合は、「条件あ」を満たしていても「当たっている」とは言えません。
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
なぜなら、もう1つの条件を満たしていないからです。もう1つの条件とは以下のようなものです。
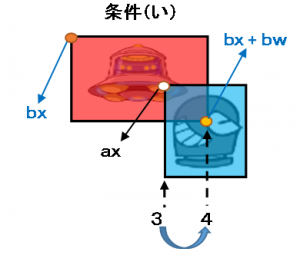
◆条件い
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
文章で書くと、矩形aの原点(ax:3番の位置)からみて、矩形bの対角(bx + bw:4番の位置)が右にある(大きい)事です。式にすると ax < ( bx + bw ) になります。これを「条件い」とします。
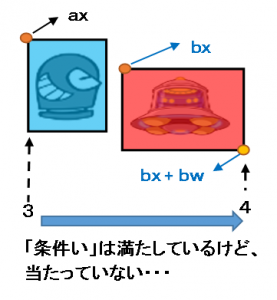
しかし「条件い」にも例外があり、下図のような場合は「当たっている」とは言えません。
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
つまり横方向だけを考えた場合、「条件あ」と「条件い」の両方を満たす必要があるわけです。
次は縦方向について考えます。縦方向では、まず以下の状態が成立するとき、当たっていると判断できます。
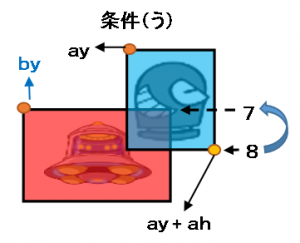
◆条件う
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
文章で書くと矩形aの対角(ay + ah:8番の位置)からみて、矩形bの原点(by:7番の位置)が上にある(小さい)事です。式にすると by < ( ay + ah ) が成り立つ時。これを「条件う」とします。
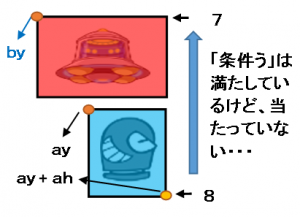
残念ながら「条件う」にも例外があります。以下の様な場合です。
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
縦の場合も「条件う」だけでは足りないのです。次の条件も満たしている必要があります。
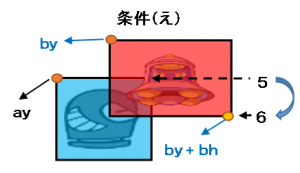
◆条件え
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
文章で書くと、矩形aの原点(ay:5番の位置)からみて、矩形bの対角(by + bh:6番の位置)が下にある(大きい)事です。式にすると ay < ( by + bh ) になります。これを「条件え」とします。
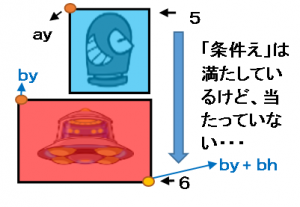
「条件え」にも例外があり、下図のような場合は「当たっている」とは言えません。
 (画像URL:illust-AC 様:うーさん、kaeru-yaさん)
(画像URL:illust-AC 様:うーさん、kaeru-yaさん)
以上の事を整理すると
- bx < ( ax + aw ) :条件あ
- ax < ( bx + bw ) :条件い
- by < ( ay + ah ) :条件う
- ay < ( by + bh ) :条件え
の4つの条件がすべて成立するとき、2つの矩形は当たっている事になります。
●その2:矩形の中心座標と幅・高さを使って判定する
上記では4つの条件を使いましたが、これをもっと簡単に済ませる事が可能です。
矩形の中心点同士の距離と、矩形の横同士の長さを利用し、以下の条件が成り立つか判定します。
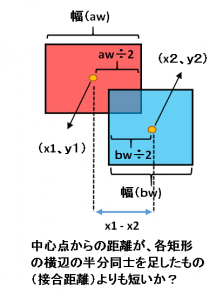
文章にすると、中心点同士の距離( x1 – x2 )が、それぞれの横辺の長さ÷2の合計( aw/2 + bw/2 )よりも短いかどうかを判定します。式にすると ABS( x1 – x2 ) < ( aw + bw )/2 となります。
ちなみに ABS() とは絶対値の事で、| x1 – x2 | と同じ意味になります。
縦方向も同様で、矩形の中心点同士の距離と、矩形の縦同士の長さを利用し、以下の条件が成り立つか判定します。
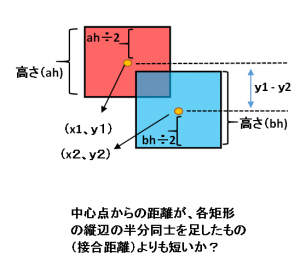
文章にすると、中心点同士の距離( y1 – y2 )が、それぞれの縦辺の長さ÷2の合計( ah/2 + bh/2 )よりも短いかどうかを判定します。式にすると ABS( y1 – y2 ) < ( ah + bh )/2 となります。
この縦と横の2つの条件
- ABS( x1 – x2 ) < ( aw + bw )/2
- ABS( y1 – y2 ) < ( ah + bh )/2
が両方とも成立するとき、2つの矩形は衝突していると判断できます。
【構文】
float f = abs( float value );
int i = abs( int value );
【パラメータ】
f / i :得られた絶対値
value : 対象数
【注意】
絶対値を求めます。求まる値は必ず正の数になります。
【関連記事】
サンプルプログラム
矩形の原点と対角座標を使って判定する例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
PImage fr1; //スイカ1 PImage fr2; //スイカ2 int px1, py1; //スイカ1の位置 int px2, py2; //スイカ2の位置 int sp1, sp2; //それぞれの速度 //初期処理関数 void setup(){ size( 400, 400 ); //イメージ読み込み fr1 = loadImage( "suika.png" ); fr2 = fr1; //座標初期化 //スイカ1は左端、スイカ2は右端 px1 = 0; px2 = width - fr2.width; py1 = (width - fr1.height)/2; py2 = py1; //速度初期化 sp1 = 4; sp2 = -4; frameRate( 60 ); } //描画処理関数 void draw(){ background( 0 ); //イメージ描画 image( fr1, px1, py1 ); image( fr2, px2, py2 ); //移動 px1 = px1 + sp1; px2 = px2 + sp2; //スイカが壁に当たったら反転 if( px1 < 0 || px1 > (width - fr1.width) ){ sp1 *= -1; } if( px2 < 0 || px2 > (width - fr2.width) ){ sp2 *= -1; } /* 衝突判定 */ if( isCollisionRect() ) { sp1 *= -1; sp2 *= -1; } } /**************************/ /* 衝突判定 */ /* 当たりなら true を返す */ /**************************/ boolean isCollisionRect(){ if( px2 < ( px1 + fr1.width ) && px1 < ( px2 + fr2.width ) && py2 < ( py1 + fr1.height ) && py1 < ( py2 + fr2.height )){ //衝突 return( true ); } return( false ); } |
上記を実行すると四角いスイカ(笑)が、水平移動しながら正面衝突します。
isCollisionRect() 関数が「矩形の原点と対角座標を使って当たり判定」する関数になります。それぞれの矩形の原点と対角座標を用いて、衝突を判定しています。
<出力サンプル>
矩形の中心座標と幅・高さを使って判定する例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
PImage fr1; //スイカ1 PImage fr2; //スイカ2 int px1, py1; //スイカ1の位置 int px2, py2; //スイカ2の位置 int cx1, cy1; //スイカ1の中心 int cx2, cy2; //スイカ2の中心 int sp1, sp2; //それぞれの速度 //初期処理関数 void setup(){ size( 400, 400 ); //イメージ読み込み fr1 = loadImage( "suika.png" ); fr2 = fr1; //座標初期化 //スイカ1は上端、スイカ2は下端 px1 = (width - fr1.width)/2; px2 = px1; py1 = 0; py2 = height - fr2.height; //中心座標 calcCenter(); //速度初期化 sp1 = 4; sp2 = -4; frameRate( 60 ); } //中心計算関数 void calcCenter(){ cx1 = px1 + fr1.width/2; cx2 = px2 + fr2.width /2; cy1 = py1 + fr1.height/2; cy2 = py2 + fr2.height/2; } //描画処理関数 void draw(){ background( 0 ); //イメージ描画 image( fr1, px1, py1 ); image( fr2, px2, py2 ); //移動 py1 = py1 + sp1; py2 = py2 + sp2; //中心再計算 calcCenter(); //スイカが壁に当たったら反転 if( py1 < 0 || py1 > (height - fr1.height) ){ sp1 *= -1; } if( py2 < 0 || py2 > (height - fr2.height) ){ sp2 *= -1; } /* 衝突判定 */ if( isCollisionRect() ) { sp1 *= -1; sp2 *= -1; } } /**************************/ /* 衝突判定 */ /* 当たりなら true を返す */ /**************************/ boolean isCollisionRect(){ if( (abs( cx1 - cx2 ) < ( fr1.width + fr2.width )/2 ) && (abs( cy1 - cy2 ) < ( fr1.height + fr2.height )/2 ) ){ //衝突 return( true ); } return( false ); } |
上記を実行すると四角いスイカ(笑)が、垂直移動しながら正面衝突します。
isCollisionRect() 関数が「矩形の原点と対角座標を使って当たり判定」する関数になります。
例1に比べて、矩形の中心座標 ( cx1, cx2, cy1, cy2 ) を管理し、中心座標と矩形の大きさを使って判定するように変更してあります。
またスイカの移動方向も、横から縦に変更しました。
<出力サンプル>
下記はサンプルプログラムをP5.jsで書き直したものです。動作イメージを確認できます。
本ページで利用しているアイコン画像は、下記サイト様より拝借しております。各画像の著作権は、それぞれのサイト様および作者にあります。


